Урок 9.
Тема «Средняя линия
трапеции»
Цели урока: проверить знания учащихся по изучаемому материалу; познакомить учащихся с понятием средней линии трапеции и теоремой о средней линии трапеции; способствовать развитию навыков решения задач с помощью новых понятий; формировать у учащихся умение находить рациональное решение задачи.
План урока:
- Организационный момент
- Контролирующий тест
- Изучение нового материала
- Закрепление материала
- Подведение итогов урока
- Постановка домашнего задания
Ход урока.
1. Организационный момент.
Приветствие, сообщение цели урока, позитивный настрой на урок.
2. Контролирующий тест /через копирку/ (два варианта, время выполнения – 10 минут). По окончании выполнения учащиеся проверяют верность выполнения, сравнивая ответы на листах с ответами, записанными на доске.
Вариант 1.
Задание: установите, истинны или ложны высказывания:
|
№ |
Высказывания |
+/- |
|
1 |
Из величин скорость и масса векторной величиной является скорость. |
|
|
2 |
Если векторы |
|
|
3 |
Векторы коллинеарны, если они противоположно направлены. |
|
|
4 |
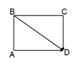
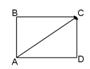
Для векторов, изображенных на рисунке, справедливо
равенство
|
|
|
5 |
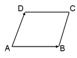
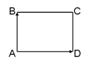
На рисунке изображен параллелограмм
|
|
|
6 |
В треугольнике АВС ВС=3 см, АВ=5 см, |
|
|
7 |
Из условия |
|
|
8 |
Верно ли равенство |
|
|
9 |
В прямоугольнике |
|
|
10* |
В прямоугольном треугольнике АВС с прямым углом С
проведена медиана СМ к стороне АВ. Если |
|
совпадают со сторонами квадрата 
, то векторы 
, 
, то 
. Тогда 
4см.
следует, что 
.
?
то 
.
Вариант 2.
Задание: установите, истинны или ложны высказывания:
|
№ |
Высказывания |
+/- |
|
1 |
Из величин сила и вес векторной величиной является сила. |
|
|
2 |
Если векторы |
|
|
3 |
Векторы называются равными, если они имеют равные длины. |
|
|
4 |
Для векторов, изображенных на рисунке, справедливо
равенство
|
|
|
5 |
На рисунке изображен прямоугольник
|
|
|
6 |
В треугольнике АВС АС=3 см, ВС=4 см, |
|
|
7 |
Из условия |
|
|
8 |
Верно ли равенство |
|
|
9 |
В параллелограмме |
|
|
10* |
В равнобедренном треугольнике АВС проведена медиана АМ к
стороне ВС. Если |
|
совпадают со сторонами параллелограмма 
5см.
следует, что 
.
?
то 
.
Ответы
|
№ |
В.1 |
В.2 |
|
1 |
+ |
- |
|
2 |
+ |
+ |
|
3 |
- |
- |
|
4 |
+ |
+ |
|
5 |
+ |
+ |
|
6 |
+ |
+ |
|
7 |
+ |
+ |
|
8 |
- |
+ |
|
9 |
+ |
+ |
|
10 |
- |
+ |
3. Изучение нового материала.
|
№ |
устно |
на доске |
|
1 |
Вспоминаем определение средней линии треугольника, теорему о средней линии треугольника |
|
|
2 |
По аналогии учащимся предлагается дать определение ср. линии трапеции и сформулировать теорему о средней линии трапеции |
|
|
3 |
Доказательство теоремы предлагается провести учащимся в группах, используя задачи, рассмотренные на предыдущем уроке. |
|
4. Закрепление материала.
№794 (фронтально, предварительно вспомнив теорему Фалеса).
5. Подведение итогов урока.
Обобщаем полученные знания, оцениваем лучшие группы учащихся по доказательству теоремы.
6. Домашнее задание: Повтор п.п.76-85; №793; №796 – слабым учащимся; №796; №797 – сильным учащимся.
_____________________________________________________________________________
